BeizerCurve

Foreword

好记性不如烂笔头。

BezierCurve简介

在数学的数值分析领域中，贝塞尔曲线（英语：Bézier curve，亦作“贝塞尔”）是计算机图形学中相当重要的参数曲线。更高维度的广泛化贝塞尔曲线就称作贝塞尔曲面，其中贝塞尔三角是一种特殊的实例。 —— 维基百科。本篇只讨论曲线。

构建Bezier曲线

线性曲线 由两个顶点构成。线性贝塞尔曲线函数中的t会经过由P0至P1的B（t）所描述的曲线。例如当t=0.25时，B（t）即一条由点P0至P1路径的四分之一处。就像由0至1的连续t，B（t）描述一条由P0至P1的直线。高阶的曲线全部基于这个线性插值。（Unity中向量的插值计算方法Vector3.Lerp可以完美实现）

线性贝塞尔曲线演示动画，t在[0,1]区间
二次曲线 由三个点构成。建构二次贝塞尔曲线，可以使中介点Q0和Q1作为由0至1的t： 1) 由P0至P1的连续点Q0，描述一条线性贝塞尔曲线。 2) 由P1至P2的连续点Q1，描述一条线性贝塞尔曲线。 3) 由Q0至Q1的连续点B（t），描述一条二次贝塞尔曲线。

二次贝塞尔曲线的结构

二次贝塞尔曲线演示动画，t在[0,1]区间
高阶曲线 建构高阶曲线，便需要相应更多的中介点。

1) 三次贝塞尔曲线

三次贝塞尔曲线的结构

三次贝塞尔曲线演示动画，t在[0,1]区间 2) 四次贝塞尔曲线

四次贝塞尔曲线的结构

四次贝塞尔曲线演示动画，t在[0,1]区间

3) 更高阶同理，需要更多的中介点，详细见代码块。

应用与代码

二次贝塞尔曲线

//pointList 为顶点集合。 point1，point2，point3 为构建曲线的三个顶点

//Vector3.Lerp 为 UnityEngine 中的API。通过传入两点和之间的插值（0~1）得到一个新的三维向量

//vertexCount 为构建曲线的顶点数，此数值越大曲线越平滑

public static Vector3[] GetBezierCurveWithThreePoints(Vector3 point_1, Vector3 point_2, Vector3 point_3, int vertexCount)
{
    List<Vector3> pointList = new List<Vector3>();
    for (float ratio = 0; ratio <= 1; ratio += 1.0f / vertexCount)
    {
        //首先取前两个点和后两个点的线性插值。

        Vector3 tangentLineVertex1 = Vector3.Lerp(point_1, point_2, ratio);
        Vector3 tangentLineVertex2 = Vector3.Lerp(point_2, point_3, ratio);
        //通过计算两个点的插值得到曲线的顶点

        Vector3 bezierPoint = Vector3.Lerp(tangentLineVertex1, tangentLineVertex2, ratio);
        pointList.Add(bezierPoint);
    }
    pointList.Add(point_3);
    return pointList.ToArray();
}

二次贝塞尔曲线unity中演示效果

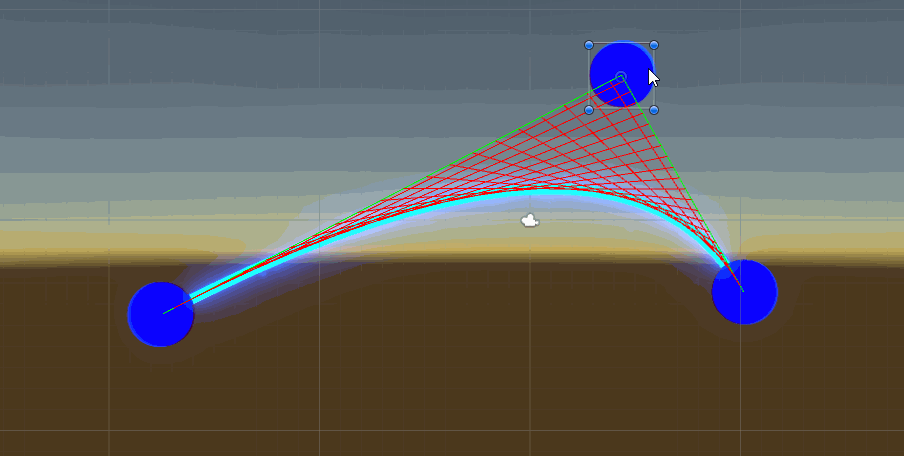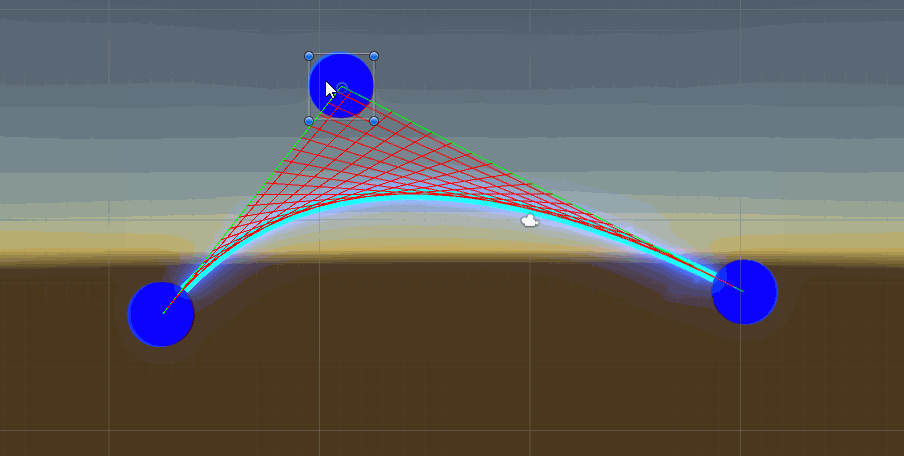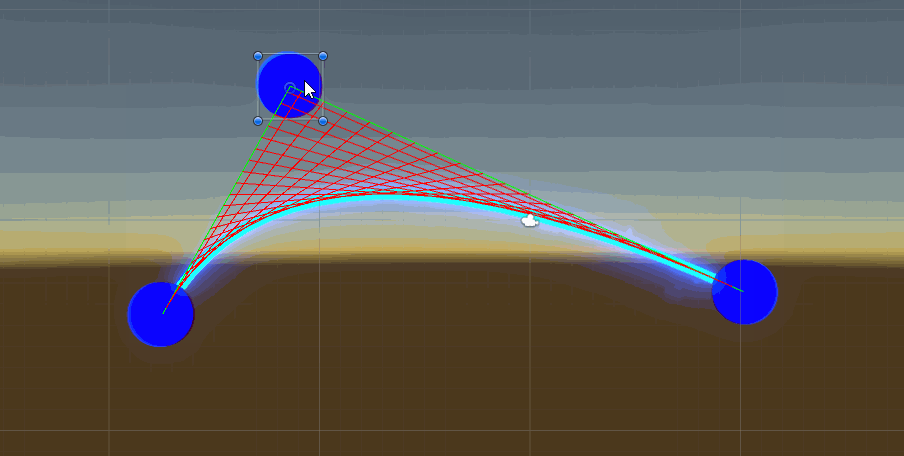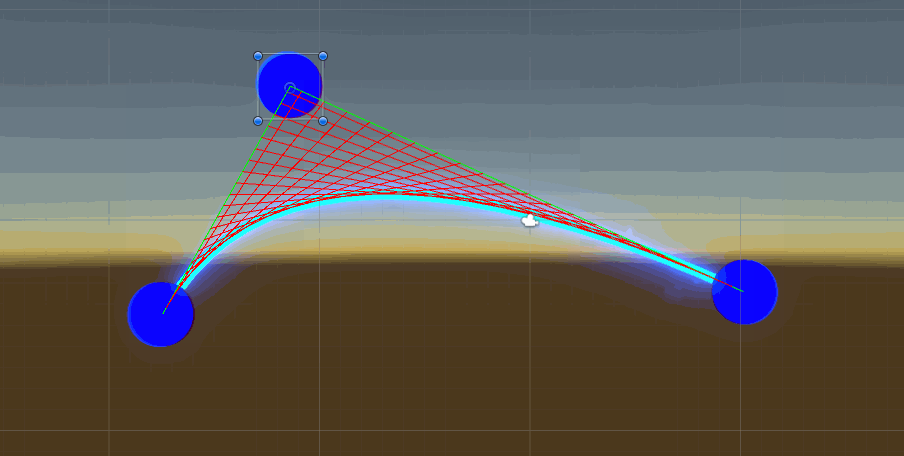
二次贝塞尔曲线演示动画

高阶贝塞尔曲线

//传入顶点集合，得到高阶的贝塞尔曲线，顶点数量不限

//vertexCount 为构建曲线的顶点数，此数值越大曲线越平滑

public static Vector3[] GetBezierCurveWithUnlimitPoints(Vector3[] vertex, int vertexCount)
{
    List<Vector3> pointList = new List<Vector3>();
    pointList.Clear();
    for (float ratio = 0; ratio <= 1; ratio += 1.0f / vertexCount)
    {
        pointList.Add(UnlimitBezierCurve(vertex, ratio));
    }
    pointList.Add(vertex[vertex.Length - 1]);

    return pointList.ToArray();
}

public static Vector3 UnlimitBezierCurve(Vector3[] vecs, float t)
{
    Vector3[] temp = new Vector3[vecs.Length];
    for (int i = 0; i < temp.Length; i++)
    {
        temp[i] = vecs[i];
    }
    //顶点集合有多长，曲线的每一个点就需要计算多少次。

    int n = temp.Length - 1;
    for (int i = 0; i < n; i++)
    {
        //依次计算各两个相邻的顶点的插值，并保存，每次计算都会进行降阶。剩余多少阶计算多少次。直到得到最后一条线性曲线。

        for (int j = 0; j < n - i; j++)
        {
            temp[j] = Vector3.Lerp(temp[j], temp[j + 1], t);
        }
    }
    //返回当前比例下曲线的点
    return temp[0];
}

高阶贝塞尔曲线unity中演示效果

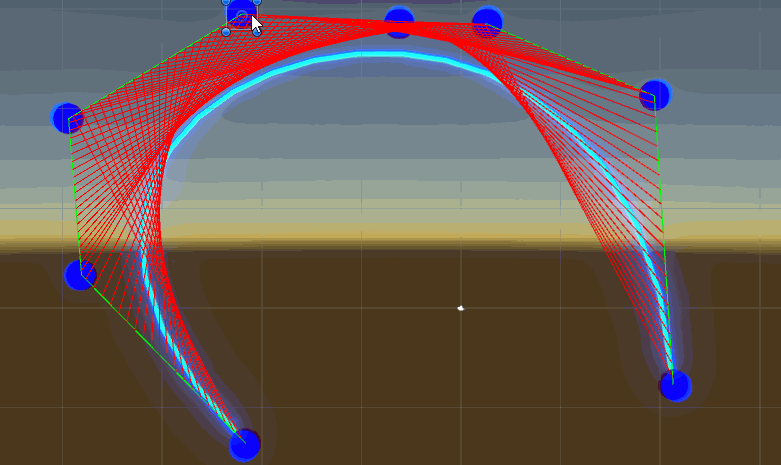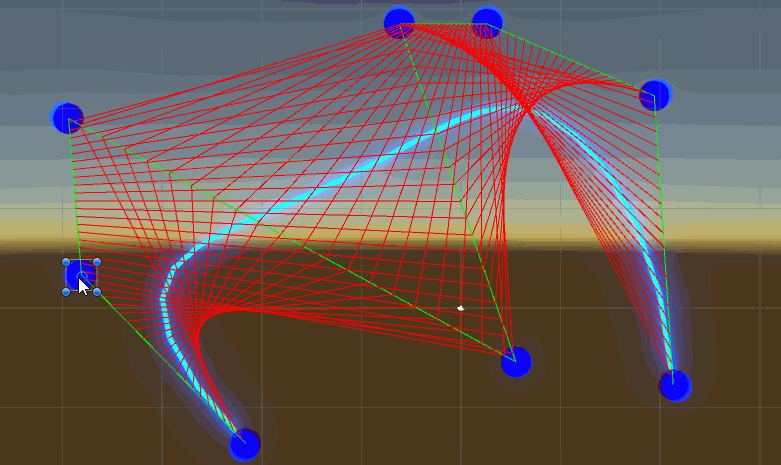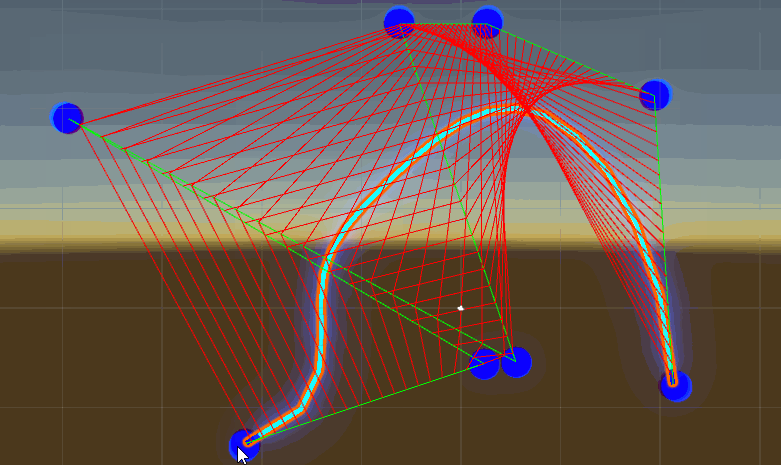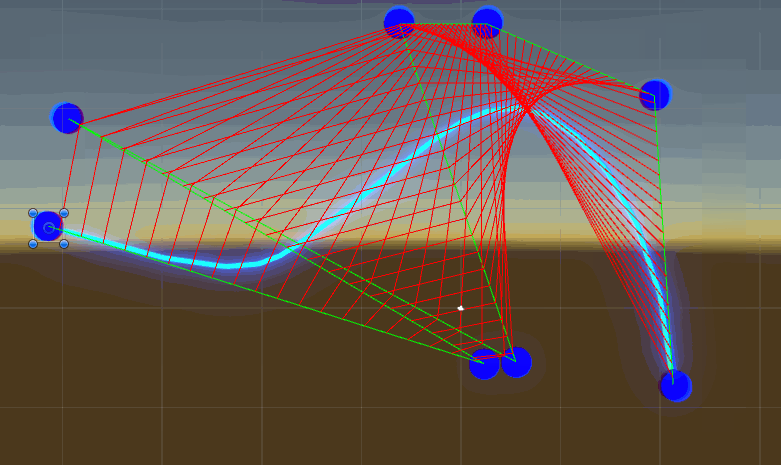
高阶贝塞尔曲线演示动画

整体脚本代码

using System.Collections;
using System.Collections.Generic;
using UnityEngine;

[ExecuteInEditMode]
public class BezierCurvePointRenderer : MonoBehaviour
{

    public Transform point1;
    public Transform point2;
    public Transform point3;
    public LineRenderer lineRenderer;
    public int vertexCount;

    public Transform[] positions;

    private List<Vector3> pointList;
    private void Start()
    {
        pointList = new List<Vector3>();
    }
    private void Update()
    {
        //BezierCurveWithThree();

        BezierCurveWithUnlimitPoints();

        lineRenderer.positionCount = pointList.Count;
        lineRenderer.SetPositions(pointList.ToArray());
    }

    private void BezierCurveWithThree()
    {
        pointList.Clear();
        for (float ratio = 0; ratio <= 1; ratio += 1.0f / vertexCount)
        {
            Vector3 tangentLineVertex1 = Vector3.Lerp(point1.position, point2.position, ratio);
            Vector3 tangentLineVertex2 = Vector3.Lerp(point2.position, point3.position, ratio);
            Vector3 bezierPoint = Vector3.Lerp(tangentLineVertex1, tangentLineVertex2, ratio);
            pointList.Add(bezierPoint);
        }
        pointList.Add(point3.position);
    }

    public void BezierCurveWithUnlimitPoints()
    {
        pointList.Clear();
        for (float ratio = 0; ratio <= 1; ratio += 1.0f / vertexCount)
        {
            pointList.Add(UnlimitBezierCurve(positions, ratio));
        }
        pointList.Add(positions[positions.Length - 1].position);
    }
    public Vector3 UnlimitBezierCurve(Transform[] trans, float t)
    {
        Vector3[] temp = new Vector3[trans.Length];
        for (int i = 0; i < temp.Length; i++)
        {
            temp[i] = trans[i].position;
        }
        int n = temp.Length - 1;
        for (int i = 0; i < n; i++)
        {
            for (int j = 0; j < n - i; j++)
            {
                temp[j] = Vector3.Lerp(temp[j], temp[j + 1], t);
            }
        }
        return temp[0];
    }

    private void OnDrawGizmos()
    {


        #region 无限制顶点数

        Gizmos.color = Color.green;

        for (int i = 0; i < positions.Length - 1; i++)
        {
            Gizmos.DrawLine(positions[i].position, positions[i + 1].position);
        }

        Gizmos.color = Color.red;

        Vector3[] temp = new Vector3[positions.Length];
        for (int i = 0; i < temp.Length; i++)
        {
            temp[i] = positions[i].position;
        }
        int n = temp.Length - 1;
        for (float ratio = 0.5f / vertexCount; ratio < 1; ratio += 1.0f / vertexCount)
        {
            for (int i = 0; i < n - 2; i++)
            {
                Gizmos.DrawLine(Vector3.Lerp(temp[i], temp[i + 1], ratio), Vector3.Lerp(temp[i + 2], temp[i + 3], ratio));
            }

        }
        #endregion

        //#region 顶点数为3

        //Gizmos.color = Color.green;

        //Gizmos.DrawLine(point1.position, point2.position);

        //Gizmos.color = Color.green;

        //Gizmos.DrawLine(point2.position, point3.position);

        //Gizmos.color = Color.red;

        //for (float ratio = 0.5f / vertexCount; ratio < 1; ratio += 1.0f / vertexCount)
        //{

        //    Gizmos.DrawLine(Vector3.Lerp(point1.position, point2.position, ratio), Vector3.Lerp(point2.position, point3.position, ratio));

        //} 
        
        //#endregion
    }
}

笔记-Unity中创建贝塞尔曲线

Foreword

BezierCurve简介

构建Bezier曲线

应用与代码

二次贝塞尔曲线

二次贝塞尔曲线unity中演示效果

高阶贝塞尔曲线

高阶贝塞尔曲线unity中演示效果

整体脚本代码

CATALOG

FEATURED TAGS

FRIENDS