前言
“It is this similarity between the whole and its parts, even infinitesimal ones, that makes us consider this curve of von Koch as a line truly marvelous among all. If it were gifted with life, it would not be possible to destroy it without annihilating it whole, for it would be continually reborn from the depths of its triangles, just as life in the universe is.” ——E. Cesaro, Atti d. R. Accademia d. Scienze d. Napoli, 2, XII, number 15. [Excerpt from an article by Paul Lévy, reprinted in Edgar’s text Classics on Fractals.]
它的整体和部分之间是相似的,即使是无穷小的部分,这使我们把冯·科赫的这条曲线看作是一个真正了不起的线条。如果它有了生命,不在初始时消灭它就不可能毁灭它了,因为它会不断地从它的三角形深处重生,就像宇宙中的生命一样。 ——E. Cesaro,Atti d。R. Accademia d。Scienze d。那不勒斯, 2,十二,第15号。[摘自PaulLévy的一篇文章,转载于Edgar的分类经典文章。]
KochCurve简介
的Koch雪花(也被称为Koch曲线,科赫星,或科赫岛[1] )是数学 曲线和最早的一个分形到已经描述的曲线。它以Koch曲线为基础,该曲线出现在1904年的一篇论文中,标题为“在没有切线的连续曲线上,可用初等几何构造”(原始法语标题:Sur une courbe continue sans tangente,obtenue par une une constructiongéométriqueélémentaire)[2]由瑞典 数学家 Helge von Koch完成。对雪花的区域中进展收敛到8/5原三角形的次数的区域,而对于雪花的周长进展发散到无限。因此,雪花具有由无限长线限定的有限区域。 —— 维基百科 。本篇只简单讨论曲线。
构建Koch曲线
-
科赫雪花可以通过从等边三角形开始构建,然后递归地改变每个线段如下:
- 将线段划分为三段等长的线段。
- 绘制一个等边三角形,其中第一步的中间部分为基础并指向外部。
- 从步骤2中删除作为三角形基部的线段。
在这个过程的一次迭代之后,最终的形状就是Hexagram的轮廓。 科赫雪花是上述步骤一遍又一遍地接近的极限。最初由Helge von Koch描述的Koch曲线只用原始三角形的三条边中的一条构成。换句话说,三条科赫曲线构成了科赫雪花。

Koch的前七个迭代

放大Koch曲线
应用与代码
构建Koch曲线
public struct LineSegment
{
public Vector3 StartPosition { get; set; }
public Vector3 EndPosition { get; set; }
public Vector3 Direction { get; set; }
public float Length { get; set; }
};
/// <summary>
/// 构建KochCurve
/// </summary>
/// <param name="position">当前图形顶点集合</param>
/// <param name="outwards">向外或向内延伸</param>
/// <param name="generatorMultiplier">延伸的比例可控</param>
protected void KochGenerate(Vector3[] position, bool outwards, float generatorMultiplier)
{
//创建线段
_lineSegment.Clear();
for (int i = 0; i < position.Length - 1; i++)
{
LineSegment line = new LineSegment();
line.StartPosition = position[i];
if (i == position.Length - 1)
{
line.EndPosition = position[0];
}
else
{
line.EndPosition = position[i + 1];
}
line.Direction = (line.EndPosition - line.StartPosition).normalized;
line.Length = Vector3.Distance(line.EndPosition, line.StartPosition);
_lineSegment.Add(line);
}
//增加线段顶点到集合中
List<Vector3> newPos = new List<Vector3>();
List<Vector3> targetPos = new List<Vector3>();
for (int i = 0; i < _lineSegment.Count; i++)
{
newPos.Add(_lineSegment[i].StartPosition);
targetPos.Add(_lineSegment[i].StartPosition);
//AnimationCurve _generatorCurve;使用Unity曲线控件,自定义曲线的变体。
//Keyframe[] _keys ,_keys = _generatorCurve.keys;获取变体的所有节点。
for (int j = 1; j < _keys.Length - 1; j++)
{
float moveAmount = _lineSegment[i].Length * _keys[j].time;
float heightAmount = (_lineSegment[i].Length * _keys[j].value) * generatorMultiplier;
Vector3 movePos = _lineSegment[i].StartPosition + (_lineSegment[i].Direction * moveAmount);
Vector3 dir;
if (outwards)
{
dir = Quaternion.AngleAxis(-90, _rotateAxis) * _lineSegment[i].Direction;
}
else
{
dir = Quaternion.AngleAxis(90, _rotateAxis) * _lineSegment[i].Direction;
}
newPos.Add(movePos);
targetPos.Add(movePos + (dir * heightAmount));
}
}
newPos.Add(_lineSegment[0].StartPosition);
targetPos.Add(_lineSegment[0].StartPosition);
_position = newPos.ToArray();
_targetPosition = targetPos.ToArray();
_bezierPosition = BezierCurve(_targetPosition, _bezierVertexCount);
_generationCount++;
}
Koch曲线变体unity中演示效果
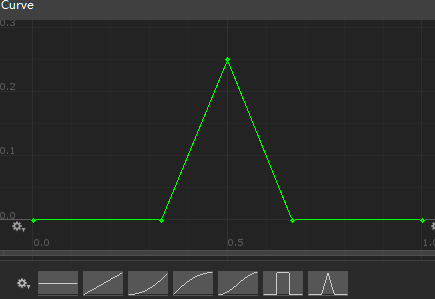
自定义变体_1
Koch曲线向外变体演示动画
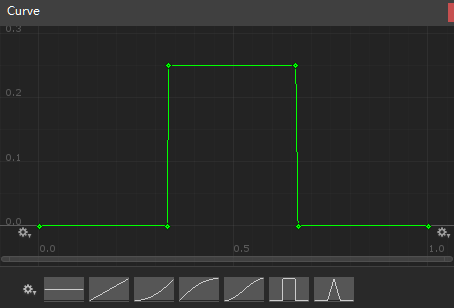
自定义变体_2

Koch曲线向外变体演示动画